Gauss Jordan Elimination Method
T he Gauss Jordan Elimination or Gaussian Elimination is an algorithm to solve a system of linear equations by representing it as an augmented matrix reducing it using row operations and expressing the system in reduced row-echelon form to find the values of the variables. The most common method that students are taught Gauss-Jordan-elimination for solving systems of equations is first to establish a 1 in position a 11 and then secondly to create 0s in the entries in the rest of the first column.

Pdf An Alternative Method To Gauss Jordan Elimination Minimizing Fraction Arithmetic Semantic Scholar
The Gauss-Jordan elimination method to solve a system of linear equations is described in the following steps.

. The best gauss jordan elimination calculator with steps does the following calculations. Rows that consist of only zeroes are in the bottom of the matrix. It consists of a sequence of operations performed on the corresponding matrix of coefficients.
The end product of Gauss Jordan elimination is a matrix in reduced row echelon form. Displays Gaussian elimination steps. This completes Gauss Jordan elimination.
To solve a system of linear equations using Gauss-Jordan elimination you need to do the following steps. A matrix is in the reduced row echelon form if the first nonzero entry in each row is a 1 and the columns containing these 1s have all other entries as zeros. What is the difference between Gauss elimination and Gauss Jordan method.
Add a scalar multiple of one row to any. Let Abe an m nmatrix. Gauss Elimination Method Gauss Jordan Method.
The method is named after Carl Friedrich Gauss 17771855 although some special cases of the methodalbeit presented without proofwere known to Chinese mathematicians as early as circa 179 CE. In this method elimination of unknowns is performed by all equations not only from equations to follow. Learn more about this method with the help of an example at BYJUS.
Multiply one of the rows by a nonzero scalar. We say that Ais in reduced row echelon form if Ain echelon form and in addition every other entry of a column which contains a pivot is zero. A The rows if any consisting entirely of zeros.
A homogeneous linear system is always. There are three elementary row operations used to achieve reduced row echelon form. Note that if one has a matrix in reduced.
In fact Gauss-Jordan elimination algorithm is divided into forward elimination and back substitution. This method can also be used to compute the rank of a matrix the determinant of a square matrix and the. The gauss Jordan calculator reduces the.
The student then performs the same process in column 2 but first a 1 is established in position a. Set an augmented matrix. Gauss elimination method is used to solve the given system of linear equations by performing a series of row operations.
Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. In mathematics Gaussian elimination also known as row reduction is an algorithm for solving systems of linear equations. Forward elimination of Gauss-Jordan calculator reduces matrix to row echelon form.
Multiply a row by any non-zero constant. After performing Gaussian elimination on a matrix the result is in row echelon form while the result after the Gauss-Jordan method is in reduced row echelon form. There exist only one difference between both.
The Gauss-Jordan method is similar to the Gaussian elimination process except that the entries both above and below each pivot are zeroed out. Both Gauss-Jordan and Gauss elimination are somewhat similar methods the only difference is in the Gauss elimination method the matrix is reduced. Where there the Gauss elimination generates the reduced.
Use row operations to transform the augmented matrix in the form described below which is called the reduced row echelon form RREF. As mentioned earlier the Gauss-Jordan method starts out with an augmented matrix and by a series of row operations ends up with a matrix that is in the reduced row echelon form. In this method the unknowns are eliminated successively and the system is reduced to an upper triangular system from which the unknowns are found by back substitution.
Write the augmented matrix of the system. To convert any matrix to its reduced row echelon form Gauss-Jordan elimination is performed. Swap the positions of two of the rows.
What is Gauss Jordan elimination method with example. The Formula used by the Gaussian Elimination Method Calculator. The Gauss Jordan Elimination is an algorithm to solve a system of linear equations by representing it as an augmented matrix reducing it using row operations and expressing the system in the reduced row-echelon form to find the solution.
The process of row reducing until the matrix is reduced is sometimes referred to as GaussJordan elimination. It relies upon three elementary row operations one can use on a matrix.

Definition Of Gauss Jordan Elimination Method Chegg Com

Solving Linear Systems With Free Variables Gauss Jordan Elimination Youtube

Gauss Jordan Elimination Reduced Row Echelon Form Youtube
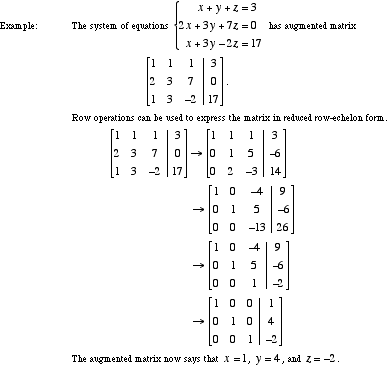
Mathwords Gauss Jordan Elimination
0 Response to "Gauss Jordan Elimination Method"
Post a Comment